写像12相をいちから勉強してatcoderの組合せ・数え上げ問題をクリアしたいと思ったけどまだまだ知らない事が多いと強烈に感じた

目的は組合せ問題にたいする苦手意識を排除しatcoderの(組合せ・数え上げのC, D問題が解けることで)スコアを伸ばすことです

私は組合せ問題がくると、自信がありません。それを克服したいのです。

写像ってなんだ？という状態です。

でも要はボールを箱に入れる時何通りある？っという問いに迷いなく答えられるようになりたいのです。

写像12相を扱った記事はいくつかあるのですが、競プロの上位の方（たとえばこれ）が書かれているものはレベルが高くて

自分がわからない部分の説明がありません。なので、初心者でも分かるような内容になればと思って書きました。

と思って始めたのですが結論から言うと

今の自分の理解のレベルでは全然理解できませんでした。さらに

「写像12相」を総整理！ 〜 数え上げ問題の学びの宝庫 〜の説明が素晴らしにつきます。最初は私が組合せ・順列の知識するら忘れている状態だったので、読めなかっただけで、そこがわかってくると如何によく調べられていて・かつ丁寧に説明されているかがわかります。といってもスターリング数、分割数、ベル数あたりの理解はもう一段階基礎知識が少ないと感じましたし、それ故に理解できていません。数え上げ＋漸化式でなんか頑張るしかないんだなー、くらいの理解にとどまっています。。。

とはいえ、現時点でいろいろなリソースから感じとった・学んだことを残しておくのは無駄なことではないと思っているので、この記事を書きました。

写像とは？

集合の対応です。私はヨビノリさんの動画とかを見ました。1対1とか1対nとかによって単射とか全射とか名前がついています。

この写像12相でも、実は一つ以下という条件は単射で、一つ以上とい条件は全射にあたります。

組合せの復習

組合せや並べ方の基本を勉強するには数学Aの復習がよかったので気になるかたはこちらのatcoderに組み合わせを問う問題が多いので復習したも参考にしてみてください。

写像12相について

その上で

やっていきましょう。

始める前のチップとして

始める前のチップとして、全ての箱において玉は一つ以下の条件では箱の数は、玉の数より多くなくてはいけません。(同じもok）

なのでk >= nという前提が入ります。

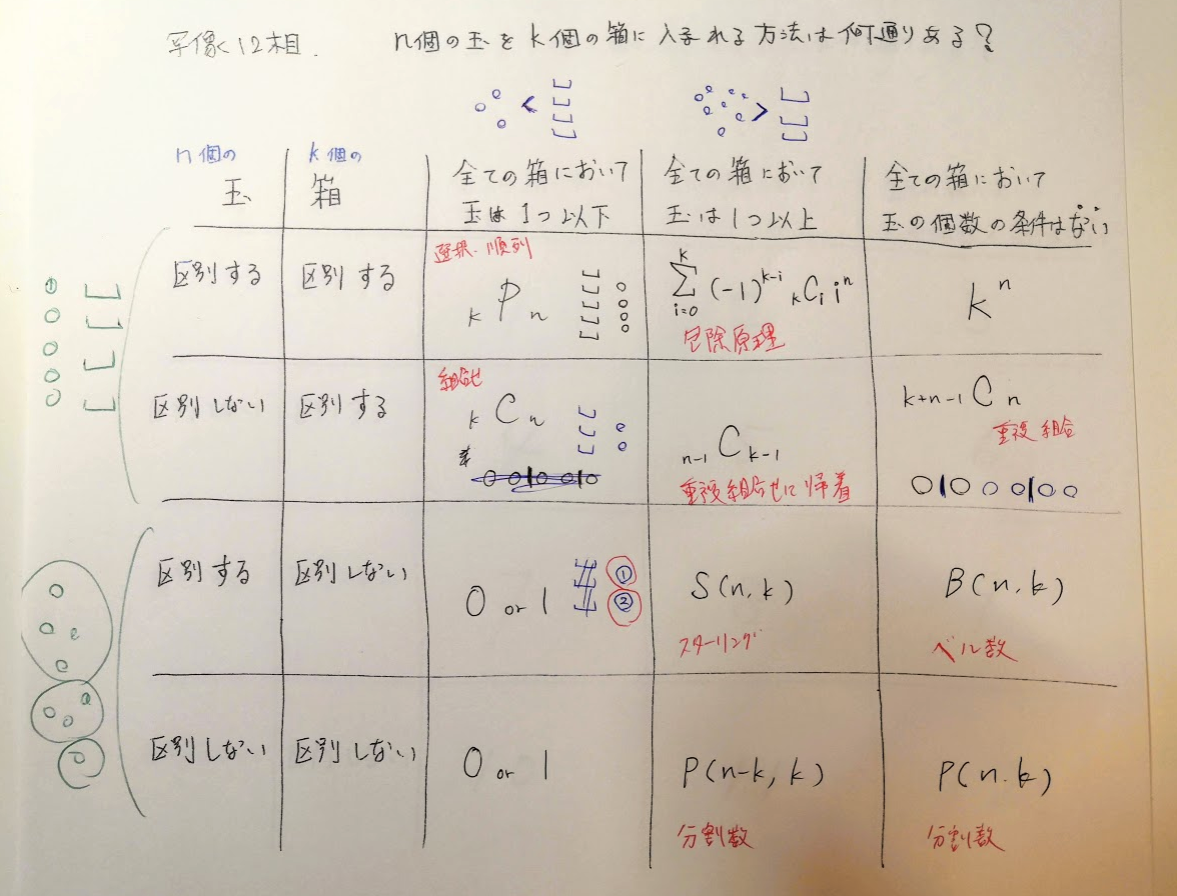
そしてこちらが早見表です。

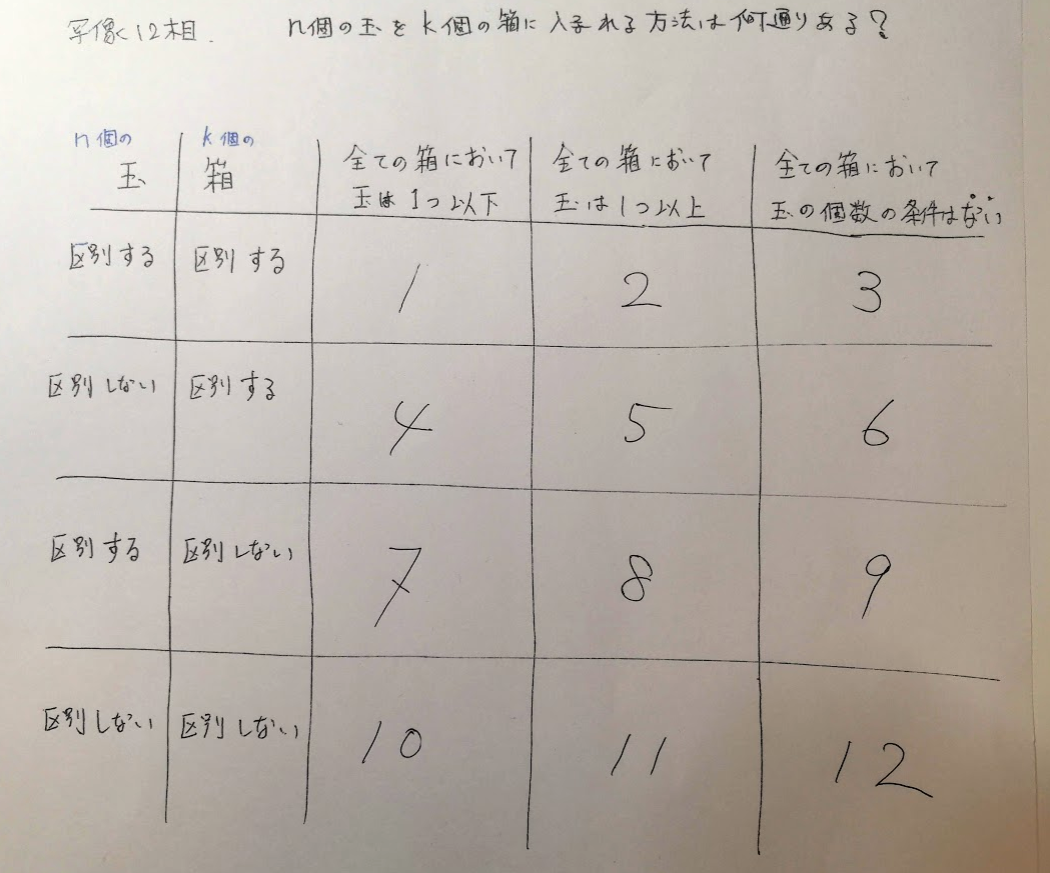
そして番号はこちらに対応します

①の玉区別する、箱区別する、全ての箱において玉は一つ以下

kPn です。

この意味は、n個からｋ個を選んだときの順列です。組合せのnCkとかは馴染みがありましたが、「Pにもそんなんあるのか！？」と思わず動揺しました。

箱の数のほうが多くないと最低１つを満たせないのでk >= nとう条件のもと考えます。

k個の箱からn個の箱を選び出して並べる方法はkPnということになります。

計算方法はwikiを見て、へー。となりました。

初等組合せ論において、n 個の元から k-個を選んで得られる順列の総数を表すのにいくつか異なる記号、例えば _nP_k, ⁿP_k, P_n,k, P(n,k) などが用いられる（同様の記法で "P" を "C" に代えたものは n-元集合の k-組合せの総数を表す）。k ≤ n のとき、その値は積 n × (n − 1) × (n − 2) × … × (n − k + 1) によって表される^[3]。一方、k > n のとき（上記の積は定義されないにも拘らず）k-順列の総数 _nP_k は単に 0 と定められる。

wiki, 記法について

②の玉区別する、箱区別する、全ての箱において玉は一つ以上

包除原理を利用する。

いきなり難しいのでてきました。説明は前述のサイトの3. 「箱を区別する場合」の残された難関を見ました。

以下の例題は、区別する、する、一つ以上の例題になっている。その解法は6C3 ・3C2・1C1の60通りとなる

(1) 6個の異なる玉を，Aさんに3個，Bさんに2個，Cさんに1個分ける方法．

https://hiraocafe.com/note/kumiwake.html

③の玉区別する、箱区別する、全ての箱において玉の個数に条件なし

一個一個n個のボールに対してk個の選択したがあるで

k*k*k...となりk^nとなります。

④の玉区別なし、箱区別する、全ての箱において玉は一つ以下

組合せ

⑤の玉区別なし、箱区別する、全ての箱において玉は一つ以上

重複組合せへ帰着

次の⑥のアイデアは箱が0でも良かったのですが、これは一つ以上

という制約があるので、予め1づつ配っておいてから分けることを

してください。

⑥の玉区別なし、箱区別する、全ての箱において玉の個数に条件なし

重複組合せ！

ときどき　のようなHがつかわれる式をみかけますが、これは重複組合せを意味します(link)

これこそ、仕切りの考え方です。

次の問題はこのカテゴリーです。以下のように３個に分けたいので２個に仕切りを置くというアプローチで行くと、

8! / (6! 2!)で解けますし、k+r-1 C rの組合せとしても解けます。

 ○　|  ○　○   |  　○　○　○

この問題は果物としていますが、果物を３個の別々のかごとして、捉えることができ、玉は区別しない。

玉を梨のかごに入れると、玉が梨に変換される、と考えてもいいでしょう。すると

 ○   ○　○   |  　○　○　|  ○

このように仕切った時に、それぞれのカゴにはいっている玉数は違うので、カゴは区別されていると考えることができます。

桃、みかん、梨の３種類の果物がたくさんあり、その中から６個果物を買う時、買い方は何通り？買わない果物があってもよい

出典：とある男が授業をしてみた　 高校数学】数A－１８組合せ⑤重複編、動画のリンクはこちら

⑦の玉区別する、箱区別なし、全ての箱において玉は一つ以下

できるか・できないかの２択

⑧の玉区別する、箱区別なし、全ての箱において玉は一つ以上

スターリング数

これがわかりやすかったです

理屈よりも、今は動的計画法として動的に倒せる

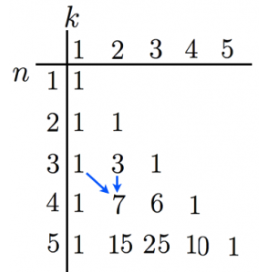
図・出典: https://mathtrain.jp/stnum

スターリング数、高校生のための計算はこれ。

⑨の玉区別する、箱区別なし、全ての箱において玉の個数に条件なし

ベル数(wiki)

⑩の玉区別なし、箱区別なし、全ての箱において玉は一つ以下

できるか、できないかの２択

⑪の玉区別なし、箱区別なし、全ての箱において玉は一つ以上

分割数

⑫の玉区別なし、箱区別なし、全ての箱において玉の個数に条件なし

分割数

この問題は⑫の区別なし、区別なし、条件なしの問題で、

サラッと、手作業で数え上げているが、理由は、公式では解けないからです。

これは分割数といわれ、自然数分割数はとけないようです。なので

漸化式でゴリゴリするのが一般的。私の今のレベルではわからない問題です。http://blog.livedoor.jp/enjoy_math/archives/50454710.html

玉６個を箱３個に分けるとき、次の場合はそれぞれ何通りだろうか。

ただし、１個も入れない箱があってもよいこととする。

①玉区別なし、箱区別なしのとき

○　○　○　○　○　○

|＿＿|　|＿＿|　|＿＿|

このときは、数えあげるのが速い。６個の玉の分け方の組合せを考えればよいので、

(6,0,0)、(5,1,0)、(4,2,0)、(4,1,1)、(3,3,0)、(3,2,1)、(2,2,2)の７通りとなる。

出典: http://www7b.biglobe.ne.jp/~math-tota/suA/tamahako.htm

別の記事では次のような説明がされています

4 ボールが区別できず, 箱も区別できない場合

さあ, いよいよ最後です. ここまでは順調に事が運んできました. しかし, 数論における未解決問題が残され ているのです. つまり, この場合において未解決問題が顔を出すのであります. (1) 各箱には高々 1 個しかボールを入れられない場合. n > r なら, ボールが余るのでダメですね. ダメ. n ≤ r なら, 手当たり次第, 目についた箱にボールを 1 個ずつ入れていって終わりです. よって 1 通りです. 先と同じ結果が出ました. こんなこともあるのです. さて, 残りの場合についてはどうでしょうか. まず, 各箱に最低 1 個はボールを入れる場合. これは、自然数 の分割という問題に絡んでいます. 自然数 n を順番を考慮しないで r 個の自然数の和として表す場合の数が, 今の問題の場合の数に等しいことは明らかです. では, それを n と r を使って上手い具合に表すことができる のかというと, 実はこれが未解決問題なのです. この場合の数を与える関数をとりあえず P(n, r) とでもおい 5 てやると, 特に制限がない場合の数, すなわち自然数 n を順番を考慮しないでいくつかの自然数の和として表 す場合の数を P(n) で表すことにすると P(n) = ∑n r=1 P(n, r) となりますが, これを有限個の有理数の和と して表す公式は発見されていません. 無限個の無理数の和として表される公式なら知られているのですが. も し P(n, r) を有限個の有理数の和として表すことができたなら, 上記のように r = 1 から n までの和を取れ ば P(n) もそのようにできるはずですが, これが未解決なのですから, P(n, r) についても未解決である, とい うことです. ここまで順調にきていたのですから, 自然な公式がないのも不自然な話です. もしかしたら, いず れは解決される問題なのかもしれません.

出典：http://www.igaris.com/math/c.pdf

こんな質問（玉も箱も区別しない組合せ）もありまして、

これは結局ｎをｍ個以下の
自然数に分割する、所謂自然数分割問題の
特殊な場合ですね。直接的な公式はまだ知られていません。ので、漸化式を使って、計算する事になります

https://oshiete.goo.ne.jp/qa/998567.html

以上です

参考・参照

黄色はこんなに数こなしてすごいです　https://tjkendev.github.io/procon-library/python/index.html

「写像12相」を総整理！ 〜 数え上げ問題の学びの宝庫 〜