問題は、三井住友信託銀行プログラミングコンテスト2019 です。
今回の学びは
C問題に53分かかっているので、スコアは低かったです。安定して20分くらいで解けるようになりましょう。
B問題は13分。A問題は5分かかっています。
これらを、早くしたい!C問題までを30分で解けるように。A->2, B-5, C->15分を当面の目標にしようか。
snukeさんは5分でC問題までACしています!。。。!
ふぁ〜、凄まじいです。DPをつかわず数学的にBFで解いています。
(動画)
B問題は、ループまわしてBFでいけるようです。なので時短だけを狙えばBF実装しちゃってもいいです。もちろん制約は一瞥してください。
c問題ですが dpでトップダウンと ボトムアップがあって 最初15分書けて書いたトップダウンはLTEでした。 ボトムアップは通りました。 よく、私はトップダウンでキャッシュする方法では通りません。 書き方がどう間違っているのかがいつも曖昧です。 こちらトップダウン
def rec(zan, dp):
# if zan % 100 == 0 or \
# zan % 101 == 0 or \
# zan % 102 == 0 or \
# zan % 103 == 0 or \
# zan % 104 == 0 or \
# zan % 105 == 0:
# print("zan {}".format(zan))
if zan == 0:
#print("hogaaaaaaaaaaaaaahhh ! {}".format(zan))
return True
elif zan < 0:
return False
else:
if zan in dp: return dp[zan]
# if zan-100 >= 0:
# a0 = rec(zan-100, dp)
# dp[zan -100] = a0
# if zan-101 >= 0:
# a1 = rec(zan-101, dp)
# dp[zan -101] = a1
# if zan-102 >= 0:
# a2 = rec(zan-102, dp)
# dp[zan -102] = a2
# if zan-103 >= 0:
# a3 = rec(zan-103, dp)
# dp[zan -103] = a3
# if zan-104 >= 0:
# a4 = rec(zan-104, dp)
# dp[zan -104] = a4
# if zan-105 >= 0:
# a5 = rec(zan-105, dp)
# dp[zan -105] = a5
a0 = rec(zan-100, dp)
dp[zan -100] = a0
a1 = rec(zan-101, dp)
dp[zan -101] = a1
a2 = rec(zan-102, dp)
dp[zan -102] = a2
a3 = rec(zan-103, dp)
dp[zan -103] = a3
a4 = rec(zan-104, dp)
dp[zan -104] = a4
a5 = rec(zan-105, dp)
dp[zan -105] = a5
#print(a0, a1, a2, a3, a4, a5)
ans = any(
[a0, a1, a2, a3, a4, a5]
)
dp[zan] = ans
return ans
def sol_topdown_but_TLE(n):
dp = [False] * (n+5)
rec(n, dp)
#print("dp[%s] = %s" % (n, dp[n]))
return '1' if dp[n] else '0'
こちらボトムアップ
def sol(n):
dp = [[False] * (n+1) for _ in range(6)]
P = [
100, # 100 yen
101, # 101 yen
102, # 102 yen
103, # 103 yen
104, # 104 yen
105, # 105 yen
]
for i in range(len(P)):
for j in range(n+1): # amount
if j % P[i] == 0:
dp[i][j] = True
else:
candidates = [False]
if j - P[i] >= 0: candidates.append(dp[i][j-P[i]])
if i - 1 >= 0: candidates.append(dp[i-1][j])
dp[i][j] = any(candidates)
#for row in dp: print(row)
#print("n {}, len(dp) {}".format(n, len(dp[0])))
return '1' if dp[5][n] else '0'
D問題のLucky PINは組み合わせの問題です。
20分ありましたが、解けそうなアイデアは浮かばずに終わりました。
翌日、動画をみました。
組み合わせは10^12くらいになるので
逆転の発想で答えが、Sに含まれるかを考える!
O(10^3)で答えの候補(T)をだしたら
TがSの部分文字列か?をダブルポインターで解く問題!
これがO(N)
じつはマップでindexをソートされている状態でもって、かつ
二分探索をするとO( LogN )でできる。と解説されていました!

あらためてatcoderは数学と発想の問題が多いな〜
という印象です。
解答を聞けば理解できるが、これをリアルタイムで発想できるよに
どうしたらよいのでしょか?。。。
数、復習。。。発想の形式化。。。
コツコツですね。
E問題。呼んですらいないですが
触ってみましょう。
さっぱりわかりません。しかし解説を聞くと理解できる。
本質は、色ではなくて分布を状態として持つことです。そして
前から処理していく。

F問題。読んですらいないですが触ってみましょう。
考え方の変換は、横軸から、二次元ぼライングラフで表すことでした。
重要なのは、このライングラフで表すとう発想です。
あかん。発想の後も場合分けが多くて、とても今の自分では解けそうにない。というのが率直な感想です。
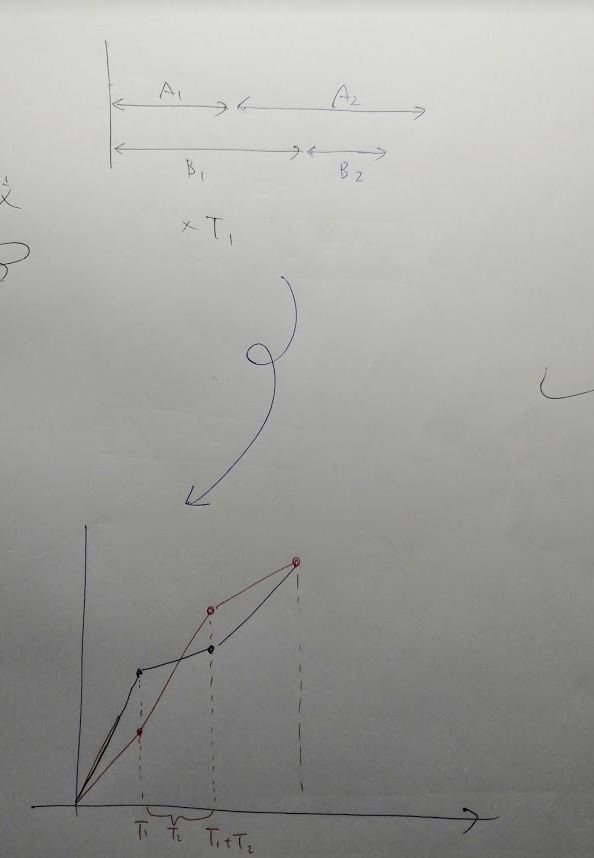
以上です