こんにちは
今回の学びは
・sliding windowは複数でも使える!といかsubarrayそれぞれにポインターを用意する秀逸さ!
・dpをより深く理解するきっかけとなった問題です
問題はmaximum-sum-of-3-non-overlapping-subarraysでhardです
(時間配分は5分問題理解 10分検討 10分実装 20分振り返り の一文45分構成)
まずは入出力をしっかりおさえましょう。
実装前後でこれは毎回書きましょう。timespace analysis (時間とスペースの分析)は
pseudocode(擬似コード)をかいてみますか。
最初15分以上考えてDPっぽいのでとけるか?

とあがきましたが、どういう状態をを持てばいいのかわからず
あきらめました。複雑なDPの場合、組み立て方が形式化されておらず、途中でギブしております。
そこでこちらのRickyさんの動画を見て
ほぉ!
windowで解けるの!?と、DPとしか考えていなかったので意表をつかれた
おもいでした。説明を聞いても、それで解けるの?
と理解できませんでしたので、写経しました。
その中で、やっと理解できました。
最初のwindowをつかった実装はこちら
class Solution:
def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:
"""
BF -> O(N^3)
"""
# https://www.youtube.com/watch?v=5pO2NbB1uJs
"""
[0,1,2,3,4,5,6,7]
[1,2,1,2,6,7,5,1], k = 2
^ ^ ^
<-------------- since lexicographically
"""
c = len(nums) - k # 8 -2 -> 6
b = c - k # -> 4
a = b - k
logging.debug("index:{} {} {}".format(c, b, a))
logging.debug("k:{} {}".format(k, nums))
sum_c = sum(nums[c:c+k])
sum_b = sum(nums[b:b+k])
sum_a = sum(nums[a:a+k])
max_c = sum_c
max_bc = sum_b + max_c
max_abc = sum_a + max_bc
logging.debug("sum:{} {} {}".format(sum_c, sum_b, sum_a))
indice_c = [c]
indice_bc = [b] + indice_c
indice_abc = [a] + indice_bc
while a != 0:
c -= 1
b -= 1
a -= 1
sum_c += nums[c] - nums[c+k]
sum_b += nums[b] - nums[b+k]
sum_a += nums[a] - nums[a+k]
if sum_c >= max_c: # equal greater to update in lexicographic order
max_c = sum_c
indice_c = [c]
if sum_b + max_c >= max_bc:
max_bc = sum_b + max_c
indice_bc = [b] + indice_c
if sum_a + max_bc >= max_abc:
max_abc = sum_a + max_bc
indice_abc = [a] + indice_bc
return indice_abc
その後、自分の解法を進めてみたいと再びDP路線でかんがえたところ
解けそうな、アイデアが固まったので実装してみます。
アイデアが解法につながったり理由は
条件で与えられた3つのサブ配列をm=3と考えて、状態をして
それを一つづつ増やしていったときの最大を求める、という風にかんがえてからでした。

この実装を写経したあとで
最初のDPももう一度考えてみました。
こんどはだいぶ、整理されています。
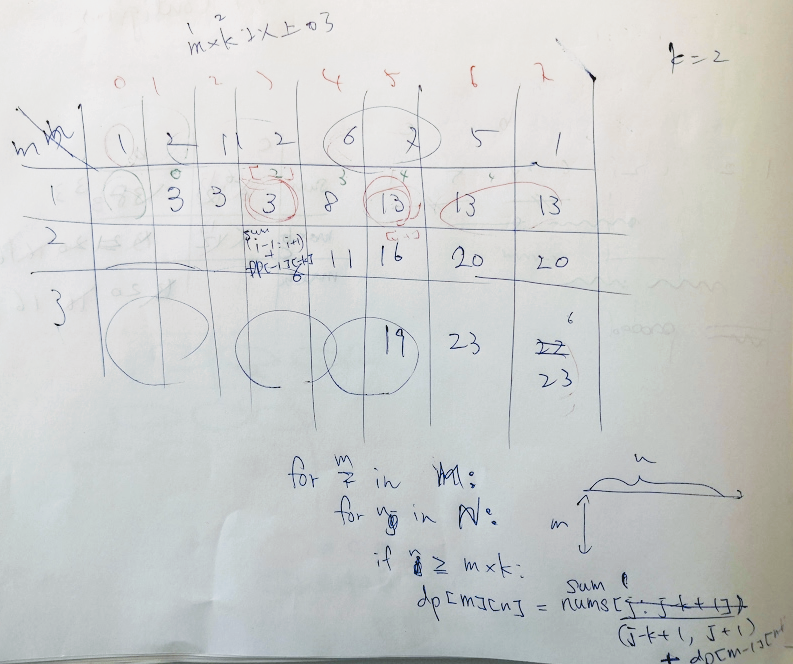
実際の実装はこちら
class Solution:
def maxSumOfThreeSubarrays(self, nums: List[int], k: int) -> List[int]:
M = 3
N = len(nums)
dp = [[0] * N for _ in range(M)]
idx = [[''] * N for _ in range(M)]
# edge case
if len(nums) < (k * M): return ans
for m in range(M):
sum_win = None
for n in range(N):
if n >= m * k:
if sum_win is None: # 何度もsumで計算するとTLEなので、その防止策(*1)
sum_win = sum(nums[n-k+1:n+1])
else:
if n-k >= 0:
sum_win += (nums[n] - nums[n-k])
else:
sum_win = sum(nums[n-k+1:n+1])
# (*1)終わり
new_val = sum_win + dp[m-1][n-k]
pre_val = dp[m][n-1]
if new_val > pre_val:
# update
dp[m][n] = sum_win + dp[m-1][n-k]
if len(idx[m-1][n-k]) > 0:
idx[m][n] = idx[m-1][n-k] + "," + "%s" % str(n-k+1)
else:
idx[m][n] = "%s" % str(n-k+1)
else:
dp[m][n] = dp[m][n-1]
idx[m][n] = idx[m][n-1]
tmp = idx[m][n]
return eval("[%s]" % re.sub(",+", ',', tmp))
最後に`eval`を入れるとう強引さはありますが
なんとか自分の考えでDPを組んでクリアすることができました。
実装後です。timespace analysis (時間とスペースの分析)は 二次元DPなので
O(N*M)ですがMはコンスタンスなのでO(N)です
「次のこの問題を解くばあい知っていればよい一つの事実とは?」
subarrayは連続値。だからsliding window使えるよ 🙂
もしくはDPでも解けるよ。
DPの考え方や解く手順などについては別途まとめたいとおもっていますが、
本記事でここまでとします。
まとめ
・sliding windowは複数でも使える!といかsubarrayそれぞれにポインターを用意する秀逸さ!
・dpをより深く理解するきっかけとなった問題です
以上です