アルゴリズム

leetcode medium meeting room ii

投稿日：

こんにちは

今回の学びは

・O(nlogn)で耐えられる入力値の目安は300万程度

・sortでkeyを使った並べ替えを覚えておこう（pythonのsortでつかわれているアルゴリズムは？=>予想はquick sortでしたが正解はtimsort(merge+insertion）でした

・問題をちょうかんたんにして一つの部屋で因数分解しながらかんがえていく

 

 

問題はmeeting room 2です

内容は[ [0, 30], [2, 10], [15, 25]]

という配列が入力で、出力は２です

同時に最大何部屋必要ですか？という問題です

メモリを気にしないと、ハッシュで時間保存していって一番太い数字を長さとかで答えられますがメモリとCPUの無駄です

O(n**2) OP(n)というパファーマンスです

なんとか操作パス一発でO(n)でまわしたいとかんがえます

[ [0, 30], [2, 10], [15, 25]]

最初はj30分まで。次は２〜１０まで

2 < 20 => duplicate ,  10 < 30 => duplicate

...

15分ほどノートとペンで考えました。

一個一個みていって最大の部屋数を更新していく、そのために最初に開始時間で配列をソートしておくというアルゴリズムです

 

実装前後でこれは毎回書きましょう。timespace anaylysis (時間とスペースの分析）は　O(nLog2n) + O(n)なのでO(logn)になります

pseudocode（擬似コード）をかいてみますか。

S = [[0, 30], [2, 10],[15, 25] ]
S.sort(S, key=lambda se1, se2: se1[0] > se2[0]) 
if S is None or len(S) == 0: return 0
max_room = 1
cur_room = 1
for i, se in enumerate(S):
  s = se[0]
  e = se[1]
  if i == 0:
    pass
  else:
    if s < dup_e: # 連続かぶりとの比較パターン
      ...
    elif s < pre_e: # 直前と比較パターン
      dup_s = max(pre_s, s)
      dup_e = min(pre_e, e)
      cur_room += 1
      max_room = max(max_room, cur_room) 
    else:
       cur_room = 1
 
  pre_s = s
  pre_e = e
return max_room

連続でかぶっている状態との比較、そうでなければ直前との比較が最大になるはずなので

そのような順番で比較すればいいんじゃないでしょうか

実際の実装はこちら

#Definition for singly-linked list.
from typing import List

class Solution:
    def minMeetingRooms(self, S: List[List[int]]) -> int:
        if S is None or len(S) == 0: return 0
        S.sort(key=lambda se: se[0])
        max_room = 1
        cur_room = 1
        dup_room = 1
        dup_s = dup_e = None
        pre_s = pre_e = None
        for i, (s, e) in enumerate(S):
            if i == 0:
                pass
            else:
                if dup_e and s <= dup_e: # 連続かぶりとの比較パターン
                    dup_s = max(dup_s, s)
                    dup_e = min(dup_e, e)
                    dup_room += 1
                    max_room = max(max_room, dup_room)
                    cur_room = 1
                elif s <= pre_e: # 直前と比較パターン
                    dup_s = max(pre_s, s)
                    dup_e = min(pre_e, e)
                    cur_room += 1
                    max_room = max(max_room, cur_room)
                    dup_room = 1
                    dup_s = dup_e = None
                else:
                    cur_room = 1
            pre_s = s
            pre_e = e
        return max_room

samples = [
    [[0, 30], [2, 10],[15, 25] ],
    [[0, 30], [2, 20],[15, 25] ],
    [[0, 14], [15, 25] ],
    [[0, 15], [15, 25] ],
    # unsorted
    [[7, 10], [2, 4] ],
    [[12, 20], [7, 10], [0, 100] ],

]
for S in samples:
    ans = Solution().minMeetingRooms(S)
    print("%s = %d" % (S, ans))

 

残念ながらこの問題は有料でロックされているのでテストケースをいくつか通ることだけ

確認して終わりにします。面接なのではこれで十分かもしれません。後で面接官が実際に大量のテストケースで

通るかどうか検証するのはまれな気がしますが、他のとの差をつけるため、ひいでたプログラマーになりたいの

であればしっかりとエッジケースやスケールの大きい入力にも対応できるコードをかきましょう

実装後です。timespace anaylysis (時間とスペースの分析）は　O(n logn )でスペースはO(1）です

ちなみに私は

O(nlogn)で耐えられる（atcoderなどでのしきい値一秒未満とか）入力値の目安は300万程度です。

O(n)の場合は1億未満としています

import numpy as np

np.log2(2**3)
3.0

np.log2(2**10)
10.0

 n = 10**6.5
 n # 10**6.5 equals to
 3162277.6601683795
 
 
 n * np.log2(n)
 68281583.52046207

さらに

別の人回答が秀逸でしたので

その考え方を紹介します

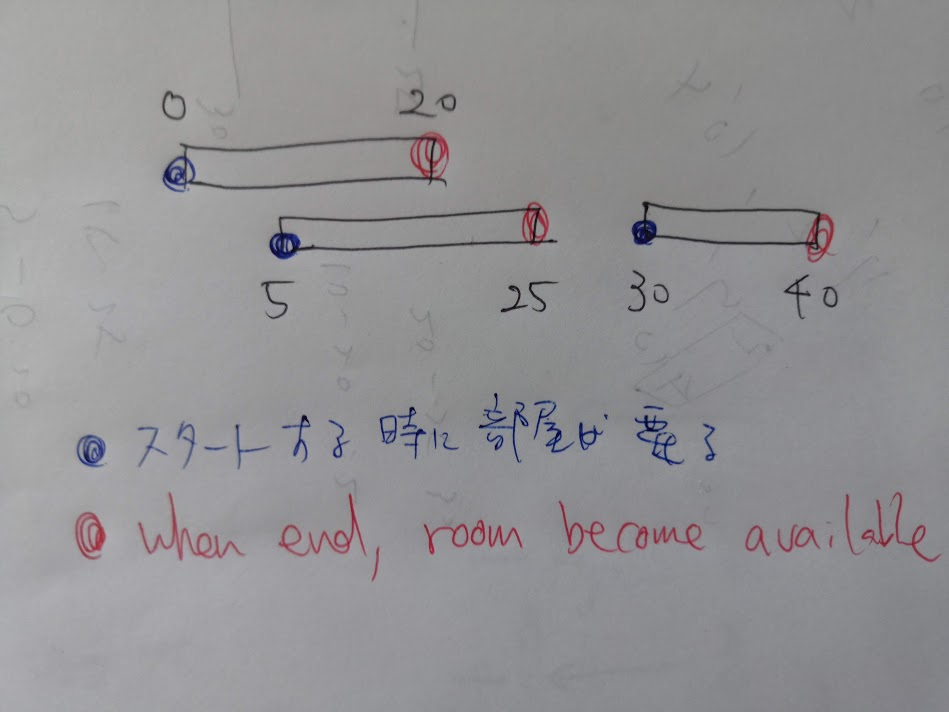
始まりの時間に常に部屋が要る　という点　終わりの時間に部屋を解放できる　という点だけを利用する

それで最大の部屋数を数えていき、開放するときには利用可能な部屋数を一個加える

利用可能な部屋があるときは、そっちを使って、最大部屋数をインクリしないとうアルゴリズム

利用可能というのは今最大でｘ必要だといっている時、ミーティングが一個終われば部屋を一個開放できてそれが

利用可能だという考え方

このアルゴリズムだと開始時刻と終了時刻を別々にソートでいきる

ソースは展示しないが、アイデアのヒントとなる図はしたのようになる

なんと行ってもポイントは始まりの時間に常に部屋が要る　という点　終わりの時間に部屋を解放できる　という点だけを利用する

という点に気づいてそれが使えるとおもえるかだ。。

おれは到底思えない。なぜそれをおもいつけるのだ。。。。

糸口は見つけられそうにないが、まずは問題をちょうかんたんにして一つの部屋で因数分解しながらかんがえていく

一つのミーティングがあるとき、必要な部屋数は１とパッとうかぶわけだが

細かく因数分解していくと始まりの時間に部屋を+1し、終了時刻に-1できるということに気づく

この特性を利用できないか？と考えることでこの紹介した解法にたどり着けるかもしれない。

まとめ

・O(nlogn)で耐えられる入力値の目安は300万程度

・sortでkeyを使った並べ替えを覚えておこう（pythonのsortでつかわれているアルゴリズムは？=>予想はquick sortでしたが正解はtimsort(merge+insertion）でした

・問題をちょうかんたんにして一つの部屋で因数分解しながらかんがえていく

以上です

-アルゴリズム

Copyright© CTOを目指す日記 , 2025 All Rights Reserved.