best-time-to-buy-and-sell-stockのシリーズの
ネタバレの記事です。自分で解きたいかたは、この記事を見ずにまずは解いてみてください。
すべての問題に共通するのは、入力とアクションです。
入力は配列、それぞれのポイントでのアクションは{buy, sell, stay}です。
そしてそれぞの問題で、
( Tはトランズアクション )
i は そして制約は T <= 1 でTは(buy->sell)をセットとしinterleaving(一個一個シークエンスに処理すること)であること。
iiは そして制約は T <= * でTは(buy->sell)をセットとしinterleaving(一個一個シークエンスに処理すること)であること。
123 iiiは そして制約は T <= 2 でTは(buy->sell)をセットとしinterleaving(一個一個シークエンスに処理すること)であること。
188 ivは そして制約は T <= k でTは(buy->sell)をセットとしinterleaving(一個一個シークエンスに処理すること)であること。
まずは、このTの制約が変わるだけで難易度がかなり変わってくる。
それはすべての問題に言えることで、組み合わせが多くなればなるほど、難易度は上がる傾向にある。
(組み合わせの復習はatcoderに組み合わせを問う問題が多いので復習した)
iiまでは比較的簡単だが、iiの動画と解説ありhttps://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/discuss/467339/Simple-solution-wvideo-whiteboard-explanation
iiiは、まずひとつ目に紹介した解法はステートごとにdpする方法で、
非常に丁寧に整理されている。
どうしても、差分で考えがちだが、一回一回のポイント{buy, sell, stay}に集中した時に
buyならprofitがマイナス方向に動くだけ、
sellならprofitが プラス方向に動くだけ
というように関数を完結させていくというポイント。と状態をうまく抽象化しているNot stock Holdingと定義しているところ。
最初のトランズアクションと二回目のトランズアクションは一方方向で別々の状態としているところ。
さらにDPでの関係性をうまく表で整理してから実装しているところがポイントです。ポイントが多いのでhard問題です。
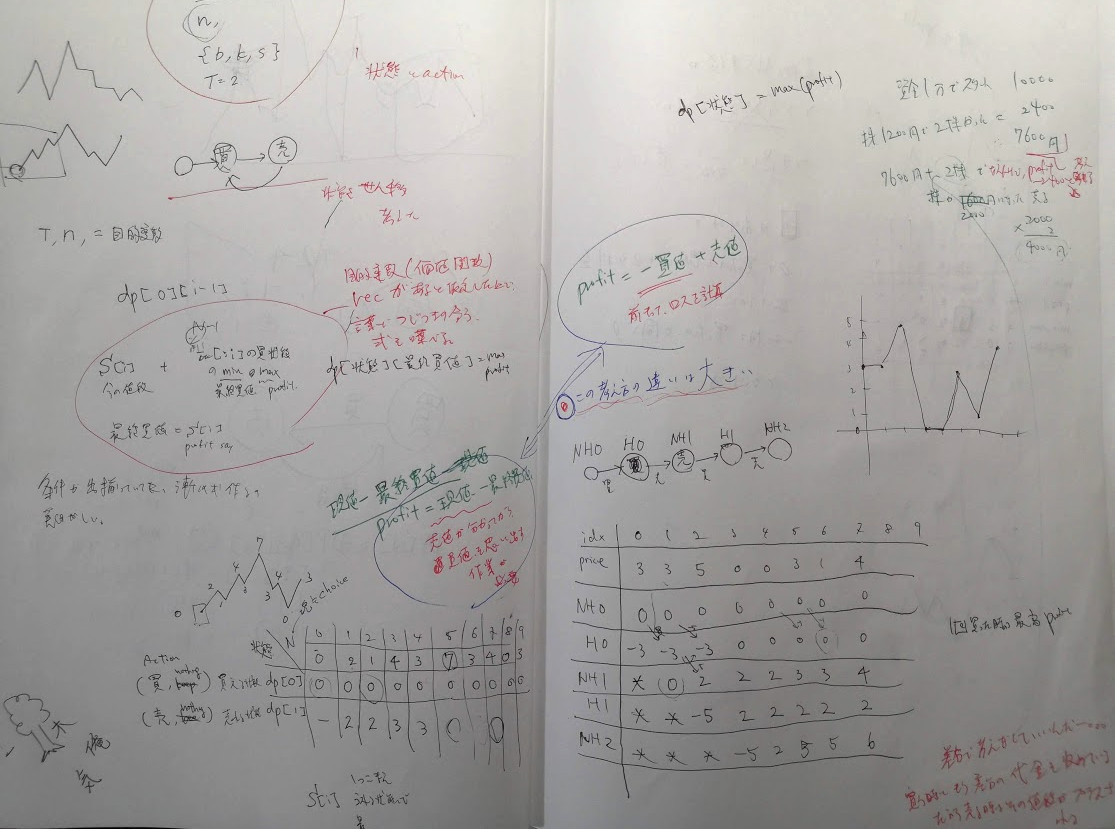
実装はこちらです。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if prices is None or len(prices) == 0: return 0
sz = len(prices)
# logic
NH0 = 0
H0 = [-sys.maxsize] * sz
NH1 = [-sys.maxsize] * sz
H1 = [-sys.maxsize] * sz
NH2 = [-sys.maxsize] * sz
for i in range(0, sz):
price = prices[i]
if i == 0: H0[i] = -price
else: H0[i] = max(-price, H0[i-1])
if i >= 1:
NH1[i] = max( H0[i] + price, NH1[i-1])
if i >= 2:
H1[i] = max(NH1[i] - price, H1[i-1])
if i >= 3:
NH2[i] = max( H1[i] + price, NH2[i-1])
# --- end ---
return max(0, NH1[i], NH2[i])
の別の解法はこちらだ
dpの複雑さからすると、何故そんなにシンプルなのか?と疑いたくなるコードだが、うまく動く。
一回目の利益をうまく次回以降の貯金として処理している。
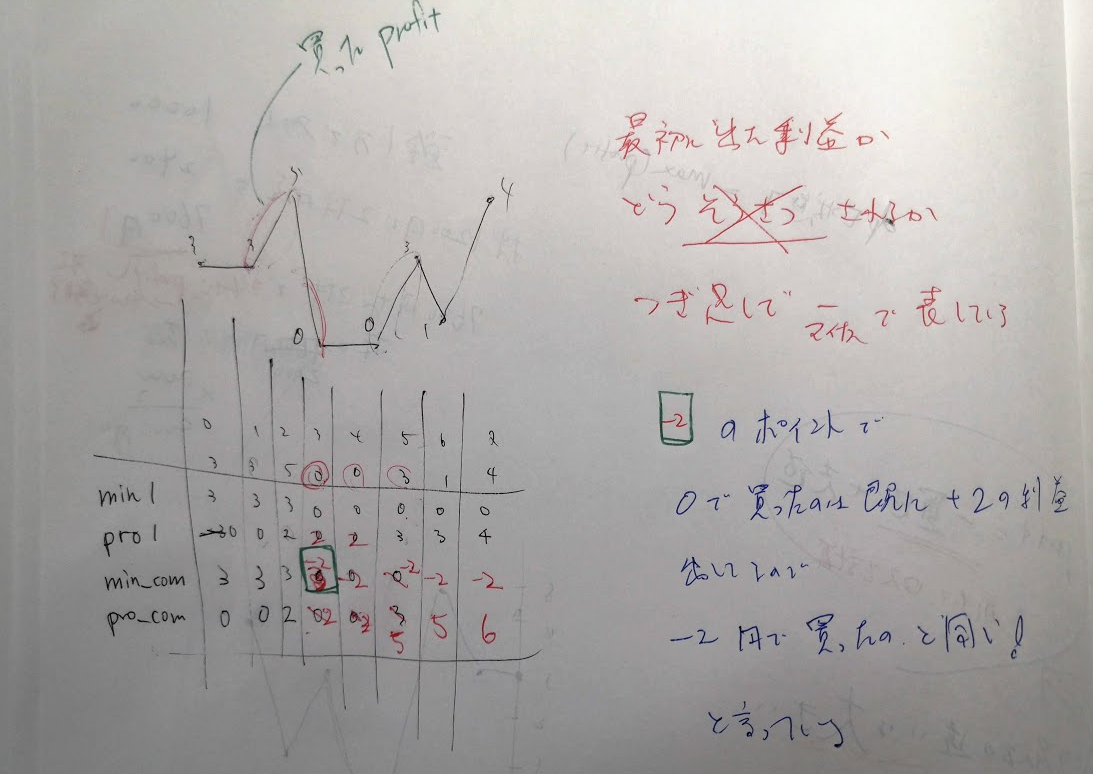
best-time-to-buy-and-sell-stock-ivはTが2から任意のkに変わっただけです。
ですから、2のコードを汎用的にするようにします。まずは前回のコードから変数を無駄dp用に撮っていた部分を削ぎ落としました。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if prices is None or len(prices) == 0: return 0
sz = len(prices)
maxi = 0
# logic
NH0 = pre_NH0 = 0
H0 = pre_H0 = -sys.maxsize
NH1 = pre_NH1 = -sys.maxsize
H1 = pre_H1 = -sys.maxsize
NH2 = pre_NH2 = -sys.maxsize
for i in range(0, sz):
price = prices[i]
NH0 = 0
H0 = max(pre_NH0 - price, pre_H0)
NH1 = max( pre_H0 + price, pre_NH1)
H1 = max(pre_NH1 - price, pre_H1)
NH2 = max( pre_H1 + price, pre_NH2)
pre_NH0 = NH0
pre_H0 = H0
pre_NH1 = NH1
pre_H1 = H1
pre_NH2 = NH2
return max(0, NH1, NH2)
だいぶスッキリしましたので、これなら汎用化できそうです。
ということで、
このように書きましたら
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
if prices is None or len(prices) == 0: return 0
sz = len(prices)
#NH = [[-sys.maxsize, -sys.maxsize]] * (k+1) # unintended reference
NH = []
for _ in range(k*2+1):
NH.append([-sys.maxsize, -sys.maxsize])
NH[0] = [0, 0]
for i in range(0, sz):
price = prices[i]
for j in range(1, k*2+1):
if j % 2 == 0:
NH[j][0] = max(NH[j-1][0] + price, NH[j][1])
else:
NH[j][0] = max(NH[j-1][0] - price, NH[j][1])
NH[j][1] = NH[j][0]
return max(0, max(cur for cur, pre in NH))
209/211 個目のテストケースでMemory Exceeded Errorとなりました。
https://leetcode.com/submissions/detail/292269953/
これは、入力が10000ということで、配列を使いすぎということです。配列に関しては直近の2個しか参照しないので、それ以前を削ぎ落とすことができそうですので、その工夫を以下に凝らします
こうしましたが、Memory超過エラーでしました。
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
if prices is None or len(prices) == 0: return 0
sz = len(prices)
#NH = [[-sys.maxsize, -sys.maxsize]] * (k+1) # unintended reference
NH = []
for _ in range(k*2+1):
NH.append([-sys.maxsize, -sys.maxsize])
NH[0] = [0, 0]
for i in range(0, sz):
price = prices[i]
for j in range(1, k*2+1):
if j % 2 == 0:
NH[j][0] = max(NH[j-1][0] + price, NH[j][1])
else:
NH[j][0] = max(NH[j-1][0] - price, NH[j][1])
NH[j][1] = NH[j][0]
# --- end ---
# for i, (cur, pre) in enumerate(NH):
# print(" HH[%s] = (%s, %s)" % (i, cur, pre))
return max(0, max(cur for cur, pre in NH))
むっちゃ難しいですね。
https://leetcode.com/submissions/detail/292269953/ 入力は1万インプットでした。
ということで、もっとスマートに実装がんばったのですが、
手こずりすぎたのでdiscussion見て、それを写経させていただきました。
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
if prices is None or len(prices) == 0: return 0
sz = len(prices)
NH = [0] * (sz + 1)
maxi = -sys.maxsize
for i in range(k):
H = [-sys.maxsize]
cur_NH= [-sys.maxsize]
for j in range(sz):
price = prices[j]
H.append(max(NH[j] - price, H[-1]))
cur_NH.append(max(H[j] + price, cur_NH[-1]))
maxi = max(cur_NH[-1], maxi)
NH = cur_NH
return max(0, maxi)
しかしながら、こんどは
209 / 211 test cases passed. LTEをくらいました。K=100000000が膨大に大きいと。
なので、Python-DP-with-detailed-explanationは冒頭にエッジケースの対応がはいっていたのですね。
ということで、その一行を追加して、はじめてクリアとなりました。
if k > len(prices): return sum(prices[i+1]-prices[i] for i in range(len(prices)-1) if prices[i+1]>prices[i])
久々に、ちょい毛が生えた問題(309. Best Time to Buy and Sell Stock with Cooldown)やりましたけどヤッパリ難しいですね、この系統は。
しかしながらとても落ち着き払った解説をありがたいです。理解に非常に役に立ちます。
class Solution:
# https://kennyzhuang.gitbooks.io/algorithms-collection/content/buy_and_sell_stock_with_cooldown.html
def maxProfit(self, S: List[int]) -> int:
if S is None: return 0
n = len(S)
if n <= 1: return 0
buy = [0] * (n+1)
sell = [0] * (n+1)
buy[0] = -S[0]
sell[0] = 0
for i in range(1, n):
sell[i] = max(sell[i-1], buy[i-1] + S[i])
buy[i] = max(buy[i-1], sell[i-2] - S[i])
return sell[n-1]
profitは売値-買値と計算しない!買った時点で -price[i]とせよ!
きれいだー
以上です