問題B https://atcoder.jp/contests/diverta2019-2/tasks/diverta2019_2_b
平面上に点が点在している、
それらを順番に追っていくとき、
あらかじめ決めたベクトルに沿った推移の場合はコストは0
それ以外は1かかる。
コストを最小に抑えよ
という問題
O(N**2)でも大丈夫な入力制限
解説はサラッと
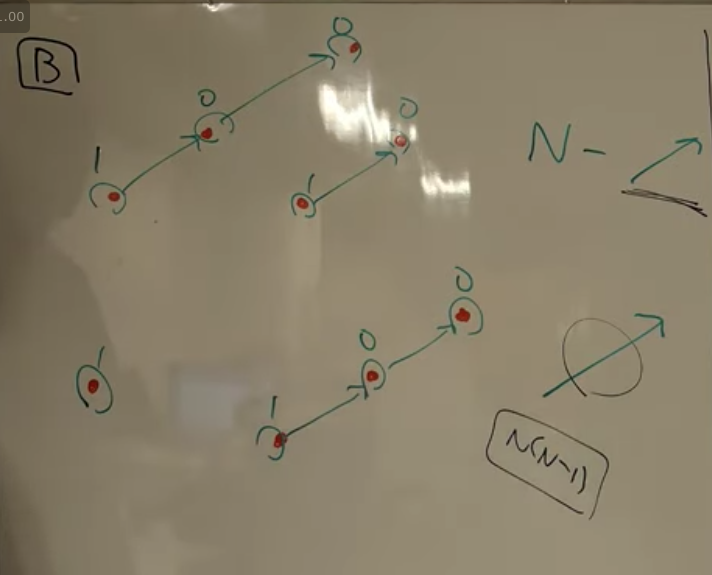
二点間の差のベクトルとして現れるものを
N(N-1)通りのベクトルを列挙して、その中でもっとも頻度の高かったものの頻度を調べる
と言っているのだが。
私は N!通りあると思って諦めていた。
最初は1を選んで、次何を選ぶかは(N-1)通り、その次に何を選ぶかは(N-2)となるから。
pdfの解説をみると納得がいった
まず、O(N**2)でp, qの候補を全て出す
それを持って
N(N-1)のループを回すと(p, q)ベクトルを持つ二点間の数を
数えることができる。
一点目から他のN-1点へのベクトルの中で(p, q)に一致するものは最大で1個しかない、それをN通りする
全体でO(N**4)のアルゴリズムとなるが
Nが50以下と小さいので50**4で62万通りと十分回せることがわかる
実装はこちら
[python]
def sol(n, S):
PQ = []
for s1 in S:
for s2 in S:
if s1 == s2: continue
PQ.append((s2[0] - s1[0], s2[1] - s1[1]))
mx = 0
for p, q in set(PQ):
tmp = 0
for s1 in S:
for s2 in S:
if s1 == s2: continue
if (s2[0] - s1[0], s2[1] - s1[1]) == (p, q):
tmp += 1
mx = max(tmp, mx)
return n - mx
[/python]
以上です。