木というデータ構造
pre-order, in-order, post-order
これらはどれも操作(traverse)の順番の違いによって名前がすこし違うだけです。
それぞれ特徴があるので覚えておくと役にたつかもです。
pre-orderは
まずはrootを処理して、そのあてLeft Subtree -> Right Subtreeと 処理します。
この順番がpre-orderです。特徴は駆らなずrootが最初に処理(visitと表現されることも、それは自由さ)されることです。
ここで
subtreeごとに処理するという概念を覚えておけさえすれば、あとは忘れても覚えていられるでしょう。
こんな感じです。
緑の点で囲った部分だけを考えて、下図の右上の順番で処理してけばいいだけです。
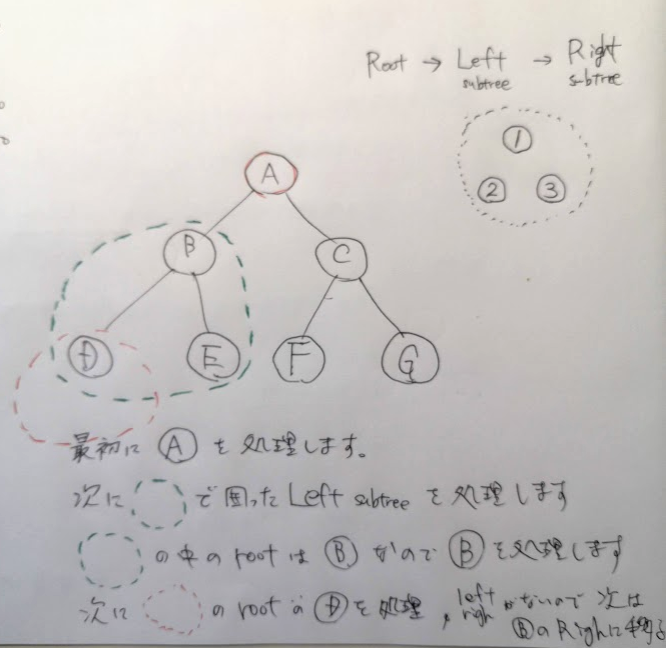
全体のイメージはこれえす。
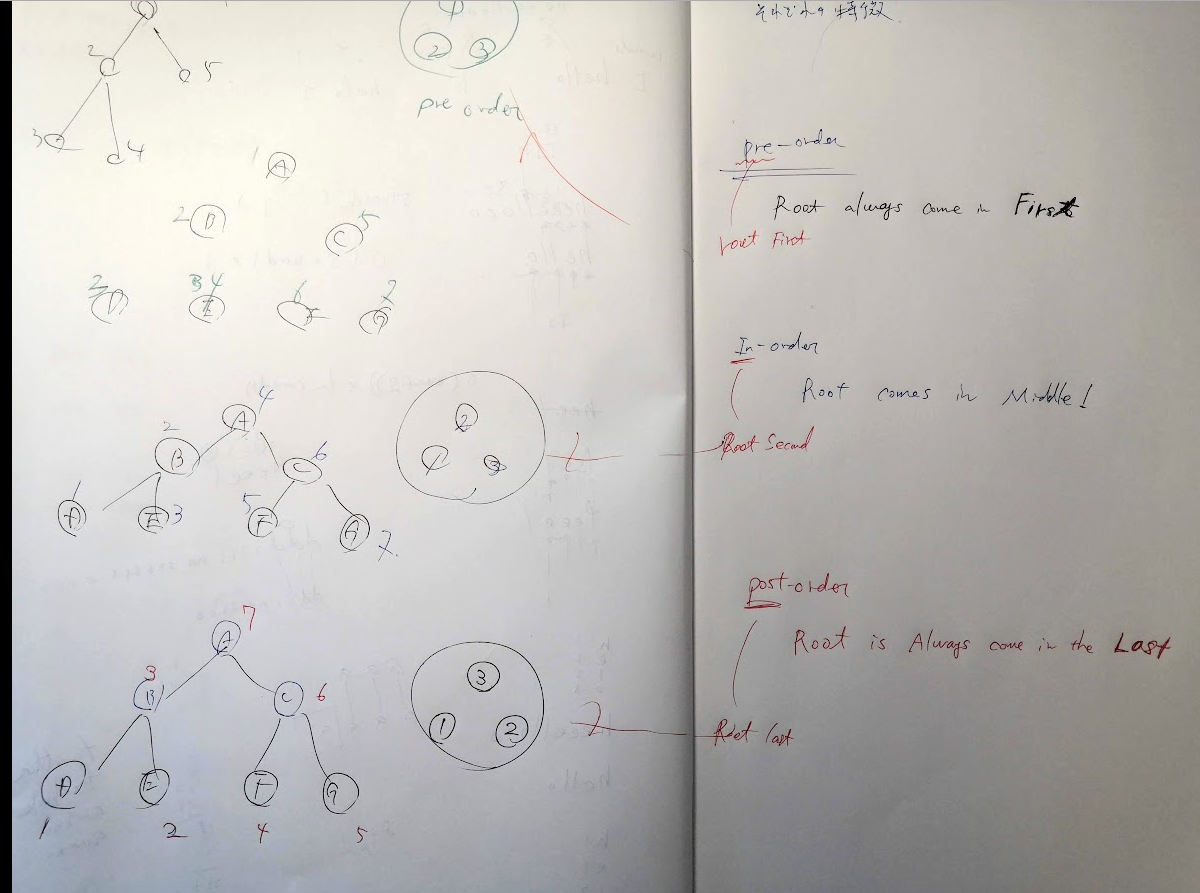
特徴としては
pre-orderの順番で値は印字していった時、必ずrootの値は最初にきます!
in-orderの順番で値は印字していった時、必ずrootの値は真ん中(くらいに分木のバランスによりけり)にきます!
post-orderの順番で値は印字していった時、必ずrootの値は最後にきます!
だから、私は
post-orderのことをroot-first-order
in-orderのことをroot-middle-order ( root-second-orderでもいいがこの名前だと2分木に限定してしまう)
post-orderのことをroot-last-order
と読んだりしています。
実践としては
leetcode - binary-tree-inorder-traversal
再起で書くとこう。私は再起でしか書けなかったですし、interativeで書こうともおもいませんでしたが
一応基本と言われているのでまずは写経です。こちらの方がleetcodeのdiscussionに実装を貼り付けてくれています。
class Solution_rec:
def __init__(self):
self.ans = []
def inorderTraversal(self, root: TreeNode) -> List[int]:
self.dfs(root)
return self.ans
def dfs(self, root: TreeNode) -> List[int]:
if root is None: return
self.dfs(root.left)
self.ans.append(root.val)
self.dfs(root.right)
ループで書くとこう
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
stack, order = [], []
curr = root
while curr or len(stack) > 0:
if curr:
stack.append(curr)
curr = curr.left
else:
curr = stack.pop()
order.append(curr.val) # inorder
curr = curr.right
return order
どちらでもかけるようにしましょう。ループのほうが処理速度が早くなっていますね。
order.appendをどこに入れるか!?によってroot-first, second, lastが変わってくる。これは再起と
一緒だけど、馴染みがない。
if curr:
###order.append(curr.val) # pre-order
stack.append(curr)
curr = curr.left
else:
curr = stack.pop()
order.append(curr.val) # inorder
curr = curr.right
###order.append(curr.val) # postorder ## No, post-order is bit more complicated
## see https://leetcode.com/problems/binary-tree-inorder-traversal/discuss/459067/Tree's-3-orders-of-traversal-solutions-in-Python-easy-understand-with-comments
post-orderのループ実装はrootノードの操作が二回目で印字するという処理をするので
すこし複雑です。
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
# Visit root in the last order , so called post-order in iterative manner
stack, order = [], []
curr = root
while curr or len(stack) > 0:
if curr:
stack.append((curr, 1))
curr = curr.left
else:
curr, visit = stack.pop()
if visit == 2:
order.append(curr.val)
curr = None
else:
stack.append((curr, 2))
curr = curr.right
return order
再起は簡単ですね。
2分木出ない場合で、複数のchildrenを持つ木構造の場合はiterativeはちょっと最初難しかったですが、
こちは、iterativeの時はstackをうまくつかう。実は再起のときも、裏では(関数呼び出しで)stackを利用しているので
その呼び出し方を意識すれば、考えられるとおもいます。関連問題はこちら【アルゴリズム脳トレ】leetcode easy 589 N-ary tree preorder traversal
【アルゴリズム脳トレ】leetcode easy 590 N-ary tree postorder traversalという問題も酷似の問題なのですが、
(追記)私は苦戦してクリアした問題ですが、もっとうまく解いている人は?
え!?これで解けるの!?と疑いたくなるくらいシンプルです。if node.childrenはNoneになりうるのでそこのvalidationをしただけで
見事に動作します。
class Solution_lc:
def postorder(self, root: 'Node') -> List[int]:
if not root:
return []
stack = [root]
self.list = []
while stack:
node = stack.pop()
self.list.append(node.val)
if node.children:
for i in node.children:
stack.append(i)
print(self.list)
return self.list[::-1]
これらのマスターとして別記事preorder, postorder, levelorderをiterativeに実装する
にまとめているのでご参考まで。
以上です
参照;
わかりやすいpre-order, in-order, post-order説明動画。https://www.youtube.com/watch?v=r3xN36so6Jg