アルゴリズム

pythonで競技プログラミングをする際のチップ

更新日：

 

gcdの最大公約数と lcm 最小公約数は　頻出だし　よく使われるので覚えておこう

lcm_listとかは3つ以上の入力について一気に処理する関数

def gcd(a,b):
    while b!=0:
        a,b=b,a%b
    return a


def lcm(a,b):
    return a*b//gcd(a,b)

def lcm_list(nums):
    if len(nums) == 0:
        return None
    if len(nums) == 1:
        return nums[0]
    if len(nums) == 2:
        lcm(nums[0], nums[1])
    else: # > 2
        a = lcm(nums[0], nums[1])
        for i in range(2, len(nums)):
            A = lcm(a, nums[i])
            a = A
        return a

事例: https://atcoder.jp/contests/abc152/tasks/abc152_e

 

 

pythonでNone判定は明示的にif x is not None:と書いて、if x:はやめよう。

理由は【アルゴリズム脳トレ】leetcode medium 64 minimum path sumでもハマったが、

上記で書いたが、入力に0がる場合にはif up: などNone判定は明示的に`if up is not None`としよう

というものでした。if 0:で意図せず条件からはずれてしまうよ。つまり最初のバグ入りの箇所は

if up and left: path = min(up, left)
elif up: path = up
elif left: path = left
else:
  path = 0

こすべきであった。

if up is not None and left is not None: path = min(up, left)
elif up is not None: path = up
elif left is not None: path = left
else: 
  path = 0

 

pythonのbisectの使い方をしっておこう

https://docs.python.org/ja/3/library/bisect.html

リストを常にソートした状態でインサートしてくれます。普通のリストでinsertしてsortするとO(NlogN)かかりますが、bisectではO(logN)です。（ただし、bisect_insortで構築されたとい前提、もしくは既にソート済。何が言いたいかというと、まぁ結局sortはO(NlogN)かかるけど、場合によってはbisect使えるよ、実装もしなくていいし。）

 

再帰の呼び出し制限はdefaultで1000なので大きくしましょう
sys.setrecursionlimit(1000000)

事例 leetcode medium 207 course schedule, atc138

 

 

inputはsys.stdin.readlineに置き換えましょう
import sys
input = sys.stdin.readline

ディフォルトのinput()より10倍早いです。無視できないです。

事例 atc138

 

お隣のペアをつくるneighboursみたな、こういう技はストックしておくと役に立つ

配列操作なのでdfsするときとかに使える。（内包表記のダブルif分はandでくくられるんだね。）

def neighbours(i, j):
  return [
    (i + a, j + b)
    for (a, b) in [(-1, 0), (1, 0), (0, -1), (0, 1)]
    if 0 <= i + a < m
    if 0 <= j + b < n
  ]

事例: number of islands,  pacific atlantic water flow

 

 

ハマった時は、入出力を見直せ。アルゴリズムを捨ててもっかいシンプルに考え直せ。

事例：入出力の考え不足、この時にいたっては考える脳の力がなかったからその思考パス(path)を掘り進めようともしなかったのが痛い真実か　【アルゴリズム脳トレ】leetcode easy 20 valid parentheses

 

口が酸っぱくなるほど行っていますが入出力はしっかりおさえること

口が酸っぱくなるほど行っていますが入出力はしっかりおさえましょう。たくさん質問しなさい

これができてないがゆえに人生の10分を何度デバッグに費やしてきたことか。。。事例を見て反省してください

事例：easy 125 valid palindrom, easy 20 valid parentheses, hard 76 minimum window substring

逆にちゃんとできて時間をセーブした事例、easy 242 valid anagram

問題文のをちゃんと理解できないまま、それに気づかず間違った前提で2日間ほど考えてしまった　hard 552 student attendance ii

 

math.ceil関数は結構遅いのでn//2 if n%2 ==0 else n//2+1とすれば二倍はやい

math.ceil関数は結構遅いのでn//2 if n%2 ==0 else n//2+1とすれば二倍はやい

事例；143 reorder list,  48 rotate image

 

 

dictに数百万単位のデータ投入は数秒のコストと心得よ

listもおんなじかなー、つまりは大量のデータの場合space のcomplexityは　time complexityに影響するということ。

事例：15 3 sum

 

 

pythonのbisectで二分検索

とりあえずググって上位ヒットした公式、とqiitaから学ぼう。

まずこのモジュールは、これ結構大事です

のモジュールは、挿入の度にリストをソートすることなく、リストをソートされた順序に保つことをサポートします

とあり、つまりは配列をソートされたまま挿入するためのモジュールです！

以下の配列に3という数字を挿入したい場合のindexはどこですか？bisect_leftなので同じ数字があった場合はその左に挿入する体で返してきます。

In [31]: bisect.bisect_left([-2, 3, 9, 12, 17], 3)
Out[31]: 1

で、４とう数字を挿入するには、どこのindexになりますか？という質問に答えてくっるクエリ系のbinary_leftは

In [32]: bisect.bisect_left([-2, 3, 9, 12, 17], 4)
Out[32]: 2

とこんな感じの仕様なので、

このままでは二分検索として使う場合には、使えません。

公式でもやっているよな、ラッパーを書く必要があります。

上記の bisect() 関数群は挿入点を探索するのには便利ですが、普通の探索タスクに使うのはトリッキーだったり不器用だったりします。以下の 5 関数は、これらをどのように標準の探索やソート済みリストに変換するかを説明します:

def index(a, x):
    'Locate the leftmost value exactly equal to x'
    i = bisect_left(a, x)
    if i != len(a) and a[i] == x:
        return i
    raise ValueError

もちろんbisect_leftは二分検索しているのでO(logN)です。https://github.com/python/cpython/blob/3.8/Lib/bisect.py

bisectは成績のマッピングにたいな用途にもピッタリです。

bisect() 関数は数値テーブルの探索に役に立ちます。この例では、 bisect() を使って、(たとえば)順序のついた数値の区切り点の集合に基づいて、試験の成績の等級を表す文字を調べます。区切り点は 90 以上は 'A'、 80 から 89 は 'B'、などです:

def grade(score, breakpoints=[60, 70, 80, 90], grades='FDCBA'):
    i = bisect(breakpoints, score)
    return grades[i]

[grade(score) for score in [33, 99, 77, 70, 89, 90, 100]]

 

事例: prampによる実践のarray index & element equalityより

 

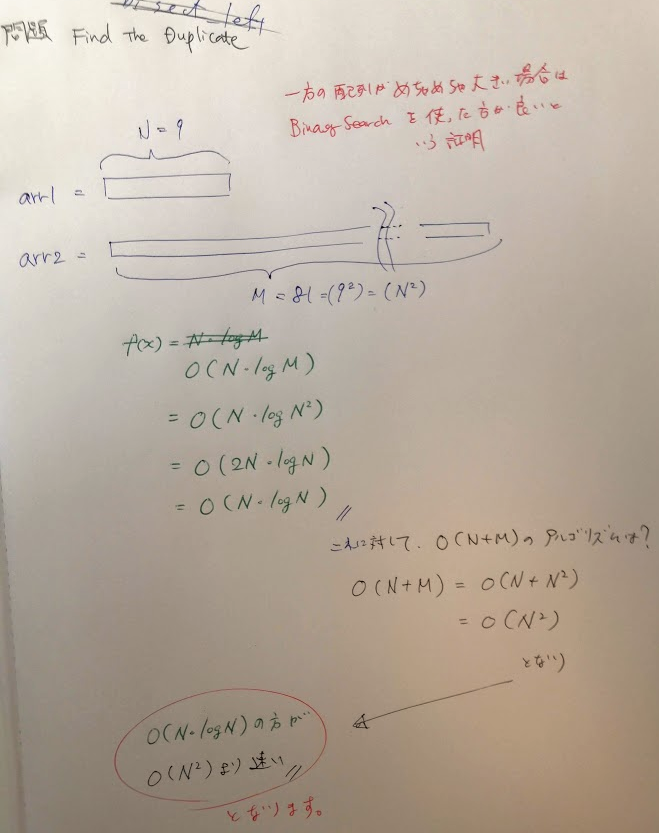
問題の入力によって、time complexityがかわってくることも！

Find The Duplicate

下で嬉しくてスクショを貼ったけど、実はこれoptimalな解法ではない。。。つまり本番であれば落とされてもおかしくない、状況です。まずは数分、binary searchが使えないか考えたい。N<<M　どちらかがめっちゃ大きい時は小さいほうで走査してbinary_searchしたほうが効率的という

その証明は以下の様にできます。以下のノートではMの配列の長さをN^2として、書いていますがN^Cのように汎用化してもいいです。M（arr2)がかなりNより大きい場合など場合によってtime complexityが変わってくることがあるということを学んだ良問だと思います。Find The Duplicateシンプルだけど奥が深くて助かります。

事例: prampによる実践のarray index & element equalityより

 

 

-アルゴリズム

Copyright© CTOを目指す日記 , 2024 All Rights Reserved.